Notes On Categories S7 Brouwer's Theorems

Balls, spheres, fixed points and retractions

The Brouwer fixed point theorems:

  1. Let I be a line segment, including its end points, and suppose that f: I -> I is a continuous endomap. Then this map must have a fixed point: a point x in I for which f(x) = x.

  2. Let D be a closed disk, and f a continuous endomap of D. Then f has a fixed point.

  3. Any continuous endomap of a solid ball has a fixed point.

The Brouwer retraction theorems:

  1. Consider the inclusion map j: E -> I of the two-point set E as boundary of the interval I. There is no continuous map which is a retraction for j.

  2. Consider the inclusion map j: C -> D of the circle C as boundary of the disk D into the disk. There is no continuous map which is a retraction for j.

  3. Consider the inclusion map j: S -> B of the sphere S as boundary of the ball B into the ball. There is no continuous map which is a retraction for j.

Let’s take an example of the relationship of the prove between those theorems. Say, If there is no continuous retraction of the disk to its boundary then every continuous map from the disk to itself has a fixed point. Brouwer did not prove this directly. Instead, Given a continuous endomap of the disk with no fixed points, one can construct a continuous retraction of the disk to its boundary.

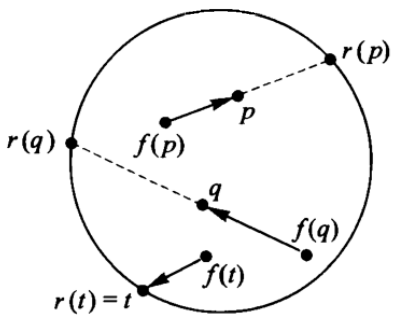
diagram for prove

Let j: C -> D be the inclusive map of the circle into the disk as its boundary, and assume we have an endomap of the disk, f: D -> D, which does not have any fixed point, that for every point x in D, f(x) =/= x. Then we build a retraction map r: D -> C such that r◦j is the identity on the circle. Draw an arrow with its tail at f(x) and its head at x, this arrow points to some point r(x) on the boundary. When x is already a point on the boundary, r(x) is x itself, so that r is a retraction for j, i.e. rj = 1C.

Some concepts:

  1. an object A (whose points are the arrows in B)
  2. a map A ->(h)-> B (assigning to each arrow its head)
  3. a map A ->(p)-> S (telling where each arrow points)

Axiom 1: If T is any object in C, and T ->(a) -> A and T ->(s)-> S are maps satisfying ha = js, then pa = s.

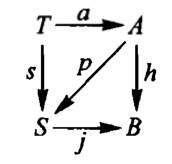
arrow diagram

Theorem 1: If B ->(alpha) -> A satisfies h◦alpha◦j = j, then p◦alpha is a retraction for j.

Corollary: If h◦alpha = 1B, then p◦alpha is a retraction for j.

Axiom 2: If T is any object in C, and T ->(f)-> B and T ->(g)-> B are any maps, then either there is a point 1 ->(t)-> T with f◦t = g◦t, or there is a map T ->(alpha)-> A with h◦alpha = g.

Theorem 2: Suppose we have maps B ->(f)-> B and B ->(g)-> B and g◦j = j, then either there is a point 1 ->(b)-> B with f◦b = g◦b, or there is a retraction for S ->(j)-> B.

Corollary 2: If B ->(f)-> B, then either there is a fixed point for f or there is a retraction for S ->(j)-> B.