Retracts and comparisons
A reasonable notation of same size is given by isomorphism: A ≅ B (read as A is isomorphic to B) means that there is at least one invertible map from A to B.
Definition: A <-> |
B means that there is at least one map from A to B. |
Definition: A is a retract of B means that there are maps A ->(s)-> B ->(r)-> A with rs = 1A, note as A <=R B.
If A and B are finite non-empty sets, A <=R B says exactly that A has at most points as B.
Idempotents as records of retracts
Suppose in sets that we have a retract A ->(s)-> B ->(r)-> A, so rs = 1A. Then we see the endomap e of B given by composing the maps r and s in the other order, e = sr, is idempotent, ee = e.
Following is the internal diagram of an idempotent map. For each point x, the point ex has to be a fixed point of e, since e(ex) = (ee)x = ex; so each point x, if not fixed by e, at least reached a fixed point in one step.
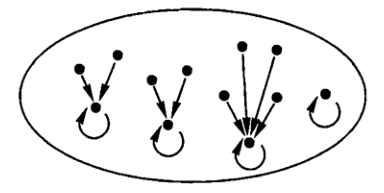
Definition: If B ->(e)-> B is an idempotent map, a splitting of e consists of an object A together with
two maps A ->(s)-> B ->(r)-> A with rs = 1A and sr = e.
Comparing infinite sets
With finite sets, we would expect that if both A <=R B and B <=R A then A ≅ B. This does not follow from just the associative and identity laws: there are categories in which it is false. Its truth for sets is the ‘Cantor-Bernstein Theorem’.
