Notice: Skip the Article III
Endomaps of sets
A simple example of a type of structure T is the idea of a single endomap T = [endomap]. A structure of that type of S is a given set with a given endomap, denoted as S[endomap]. And X[alpha] is an object of the category S[endomap]. A map f from objects X[alpha] -> Y[beta] should satisfy X ->(f) -> Y and f◦alpha = beta◦f. The composition of the maps is as X[alpha] ->(f)-> Y[beta] ->(g)-> Z[gamma], and X[alpha] ->(g◦f)-> Z[gamma]. And the identity map is X[alpha] ->(1X)-> X[alpha].
Paradoxically, many categories of structures are built from sets, which have no structure. Although an abstract set is completely described by a single number, the set has the potentiality to carry all sorts of structure with the help of maps.
Two subcategories: Idempotents and automorphisms
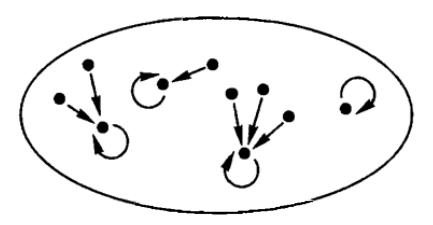
The category S[idempotent] of sets with an endomap which is idempotent contains the object X[alpha] with alpha◦alpha = alpha. An isomorphism in S[idempotent] means “correspondence between fixed points and correspondence between branches at corresponding fixed points.” Below is a picture of an object in S[idempotent]:
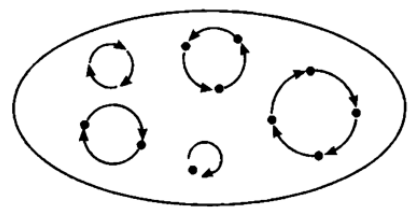
The category S[invertible] of sets with an endomap which is invertible contains the object X[alpha] with alpha is invertible, i.e. a map beta such that alpha◦beta = 1X and beta◦alpha = 1X. Recall that an endomap which is also an isomorphism is called an automorphism. An automorphism of an finite set is also known as a permutation of a set. Below is a picture of an object in S[invertible], it can have circles of any length, but no branches:
The category of graphs
S[pair map] is the supercategory of S[endomap]. An object in S[pair map] is a pair of maps with the same domain and codomain. Thus an object in S[pair map] consists of two sets X, Y, and two maps s and t (called ‘source’ and ‘target’) from one to the other.
Such a thing is called a graph. (In this case, it is of irreflexive directed multigraphs.)
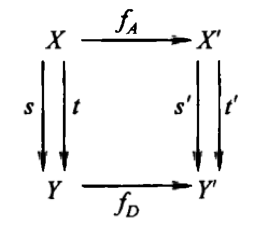
Definition: A map in S[pair map] from X =>(s,t)=> Y to X’ =>(s’,t’)=> Y’ is a pair of maps of sets,
X ->(fA)-> X’, Y ->(fD)-> Y’ such that fD◦s = s’◦fA and fD◦t = t’◦fA.