Sorting of the domain by a property
For a general map X -> (g) -> B, g gives rise to a sorting of X into B sorts.
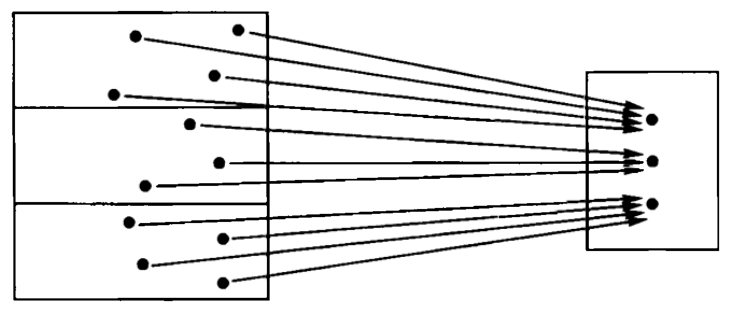
The map g is a B-valued property on X. The map g is a stacking of the elements of X into B stacks.
X is divided into B fibers. While partitioning is more restricted, no sort is empty. All of these
terms emphasize that a given map X -> B produces a structure in the domain X, and when we want to
emphasize this effect we may refer to the map itself as a B-valued property.
Naming or sampling of the codomain
Given a map A -> (f) -> X, we can say that f is a family of A elements of X.
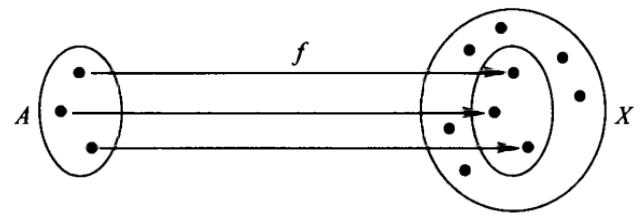
f is a family of three elements of X. A map from A to X is an A-shaped in X. We can also say A-element.
An ancient principle of mathematics holds that a figure is the locus of a varying element. An A-parameterized
family A -> X is a varying element, in that (a) if we evaluate it at various 1 -> A, we will vary it through
various points of X, but also in that (b) we can also replace the special 1 by D, thus deriving from the
given map A -> X a family of D-elements of X, one for each D -> A. For example, we can take D = A, and the
identity D -> A, thus revealing that (c) the varying element, as a single thing, is a single figure or
element itself.
We can also say that a map A -> X is a naming of elements of X by A, or a listing of elements of X by A. The word listing usually has the connotation of order, this is not the case in the discussion. We also say that to give f: A -> X is to parametrize or exemplify part of X by moving along A following f.
All of the above terms emphasize that a map A -> X produces a structure in the codomain X. When we want to emphasize this effect, we may refer to the map itself as an A-shaped figure (or as an A-parametrized family) in the codomain.
Philosophical explanation of the two aspects
There is a special part of reality has a special relationship wit reality, to reflect it. Thinking, the
result of this reflective process is knowledge, and the totality of accumulated knowledge with its inner
relationships is science. Science is a complex of interrelated sciences focusing on different aspects of reality.
One of the particular sciences is philosophy, reflecting this particular relationship within reality, the relationship between thinking and reality. Thus within the complex of all scientific thinking there is the particular relation between objective and subjective:
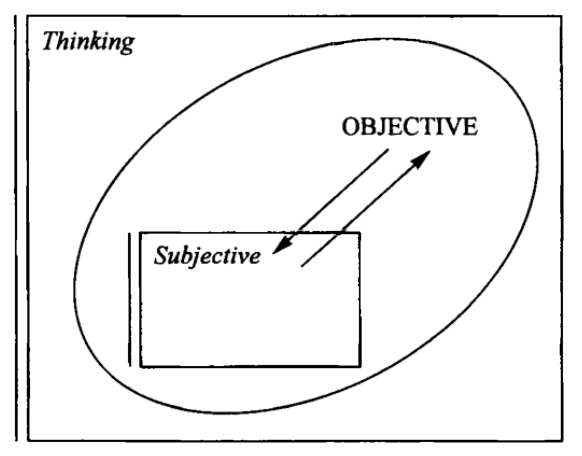
In the objective, we strive to have as clear an image as possible of reality, as it is and moves in itself, independent of our particular thoughts; in the subjective we strive to know as clearly as possible the laws of thinking in itself, arriving at laws of grammar, of pure logic, of algebra, etc.
Uses of isomorphisms
A principle use of isomorphisms is to give coordinate systems. And there are two fundamental errors to avoid. The first abuse is to assume that an isomorphism of sets A -> X means that some additional structure that A has will be meaningful in X. The second abuse involves one object A and two objects X and Y coordinatized by A. For example, adding two objects such as the distances and the masses. It only appeared to make sense they are separately identified with the object numbers, by choosing a unit of measurement for each.
