Composition of maps is analogous to multiplication of numbers, and we try to find the analog of the division of numbers.
Inverses versus Reciprocals
That the reciprocal for numbers has the corresponding notion for composition
of maps, inverse.
Definition: If A -> (f) -> B, an inverse for f is a map B -> (g) -> A satisfying
both g◦f = 1A and f◦g = 1B.
If f has an inverse, we say f is an isomorphism, or invertible map.
Uniqueness of inverses: Any map f has at most one inverse.
Isomorphisms as divisors
The process of the following maps by a particular isomorphism is itself a reversible process.
Other Stuffs
In Euclid’s category, an object is any polygonal figure which can be drawn in the plane, and a map f from a figure F to a figure F’ is any map f of sets which preserves distances: if p and q are points of F, then the distance from fp to fq in F’ is same as the distance from p to q. Isomorphic objects in this category are called by Euclid congruent figures.
In topology, sometimes loosely referred to as rubber-sheet geometry, maps are not required to preserve distances, but only to be continuous: very roughly, if p is close to q then fp is close to fq. Isomorphic objects in this category are saied to be homeomorphic.
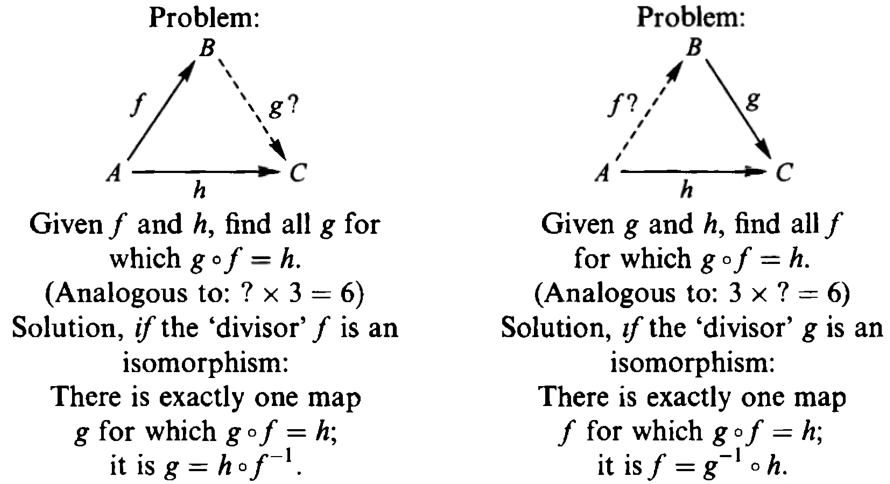
Determination Problems
Determination problem is: Given maps f from A to B and h from A to C, find
all maps g from B to C such that g◦f = h.
Constant Maps
Suppose B is a one element set, f takes all elements of A to the only element of B, map h should take all elements of A to one element of C so as to have a solution in the determination problem. Such a map is called a constant map.
Definition: A map that can be factored through 1 is called a constant map.
Choice Problems
To find a f such that g◦f = h.
Two special cases of division: sections and retractions
Definition: A -> (f) -> B is a section of B -> (g) -> A if g◦f = 1A.
One of the most important applications of a section is that it permits us to give a solution to the chocie problem for any map A -> (h) -> C. That f = s◦h.
The number of sections often differs from the number of solutions of the choice problem.
Similar for retractioins and determination problems.
If we have s◦f = 1A, then s is the only section of f, and it is called the inverse of a.
