Isomorphisms
Definition: A map A -> (f) -> B is called an isomorphism, or invertible map,
if there is a map B -> (g) -> f for which g◦f = 1A and f◦g = 1B. And g is called
an inverse for f. Two objects A and B are isomorphic if there exists at least
one isomorphism A -> (f) -> B.
The notation of isomorphic (or equinumerous, same size) has following properties:
- Reflexive: A is isomorphic to A.
- Symmetric: If A is isomorphic to B, then B is isomorphic to A.
- Transitive: If A is isomorphic to B and B is isomorphic to C, then A is isomorphic to C.
Notation on the inverse of a map: If A -> (f) -> B has an inverse, then the
inverse of f is denoted by f-1.
Two important things:
- To show that a map B -> (g) -> A satisfies g = f-1, you must show that g◦f = 1A and f◦g = 1B.
- If f does not have an inverse, then f-1 does not stand for anything.
General division problems: determination and choice
The determination (or extension) problem: Given f and h as shown, what are
all g, if any, for which h = g◦f.
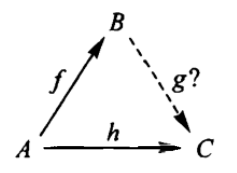
The choice (or lifting) problem: Give g and h as shown, what are all f, if
any, for which h = g◦f.
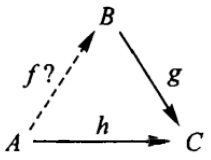
In the determination problem and the choice problem, when h is an identity map, they turn out to be retraction problem and section problem.
Definitions: If A -> (f) -> B, a retraction for f is a map B -> (r) -> A for
which r◦f = 1A, and, a section for f is a map B -> (s) -> A for which f◦s = 1B.
If a map has sections, it may have several, and another map may have several retractions. Some maps have retractions but no sections (or vice versa), and many have neither.
Proposition: If a single choice problem has a solution (a section for f), then
every choice problem involving the same f has a solution.
Proposition 1: If a map A -> (f) -> B has a section, then for any T and for any
map T -> (y) -> B there exists a map T -> (x) -> A for which f◦x = y.
If a map f satisfies the conclusion of above proposition, it is often said to be
surjective for maps from T.
Since among the T there are the one-element sets, and since a map T -> (y) -> B from a one element set is an element, so if the codomain B of f has some element which is not the value f◦x at any x in A, then f could not have any section s.
Proposition 1*: If the single determination problem has a solution (a retraction
for f), then every determination problem with the same f has a solution.
Proposition 2: If a map A -> (f) -> B has a retraction, then for any set T and
any pair of maps T -> (x1) -> A, T -> (x2) -> A from any set T to A, if f◦x1 = f◦x2,
then x1 = x2.
If a map f satisfies the conclusion of above proposition, it is said to be injective for maps from T.
If f is injective for maps from T for every T, one says that f is injective, or is a monomorphism.
Since T could have just one element, if there were two elements x1 and x2 of A for which x1 =/= x2 yet f◦x1 = f◦x2, then there could not be any retraction for f.
Definition: A map f with the cancellation property (if t1◦f = t2◦f, then t1 = t2)
for every T is called an epimorphism.
Both monomorphism and epimorphism are cancellation properties.
Proposition 3: If A -> (f) -> B has a retraction and B -> (g) -> C has a retraction,
then A -> (g◦f) -> C has a retraction.
Definition: An endomap e is called idempotent if e◦e = e.
Theorem (uniqueness of inverses): If f has both a retraction r and a section s,
then r = s.
Isomorphisms and automorphisms
Definitions: A map f is called isomorphism if there exists another map f-1
which is both a retraction and a section for f. Such a map f-1 is called the
inverse map of f. The theorem of the uniqueness of inverses shows that there
is only one inverse.
A map which is both an endomap and at the same time an isomorphism is called an
automorphism.
If there are any isomorphisms A -> B, then there are the same number of them as
there are automorphisms of A. (*p. 69)
An automorphism in the category of sets is traditionally called a permutation.
