Notes On Categories S2 Sets And Maps

Basic components of category

In this category, an object is a finite set or collection. (Usually the order of elements in the set is not important.) We scatter the elements in the set as following picture. The picture, labeled or not, is called an internal diagram.

In this category, a map f consists of three things:

1. a set A, the domain of the map
2. a set B, the codomain of the map
3. a rule, assigning to each of element a in the domain, exactly one element b in the codomain. b is denoted by f◦a.

(Other words for map are function, transformation, operator, arrow and morphism)

Following is the internal diagram of map. For any map, there is an arrow leaving from each element in the domain to a corresponding element in the codomain.

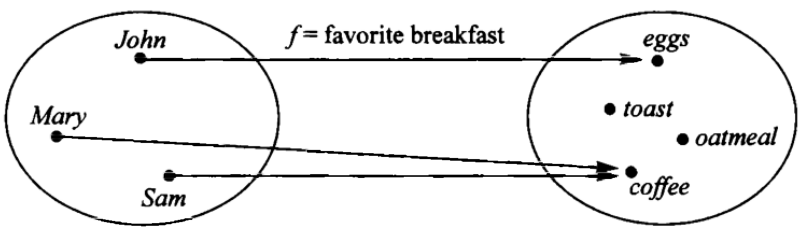
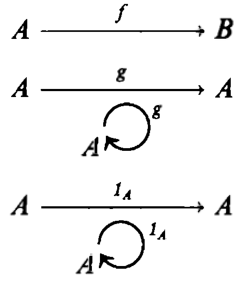
An endomap is the map where the domain and the codomain are the same object.

The identity map is a special endomap where for any a in the domain, we have f◦a = a.

Following is the external diagram which is useful when the exact details of the maps are temporarily irrelevant or we have several objects and maps.

)

The composition of maps combines two maps to obtain a third map.

To have a category, all the basic ingredients needed are objects, maps, identity maps(one per object) and composition of mapss.

Rules for category

1. The identity rule:
   1. If A -> (1A) -> A -> (g) -> B, then A -> (g◦1A) -> B
   2. If A -> (f) -> B -> (1B) -> B, then A -> (1B◦f) -> B
2. The associative rule: If A -> (f) -> B -> (g) -> C -> (h) -> D, then A -> ((h◦g)◦f = h◦(g◦f)) -> D

Definition: A point of a set X is a map 1 -> X.

A point is a map. Composing a point with another map produces another point.

Other stuffs

Test for equality of maps of sets A -> (f) -> B and A -> (g) -> B: If for each point 1 -> (a) -> A, we have f◦a = g◦a, then f = g. (Notice: Of course the domain and the codomain of the maps should be the same.)

Composition of maps

The number of maps from a set A to a set B is #(B ^ A) = #B ^ #A