Parts and stable conditions
A condition is called stable for any figure x in X with shape A that satisfies the condition and for any A’ ->(alpha)-> A, the transformed figure x’ = x◦alpha also satisfies the condition.
Definition: x is in g (or x belongs to g) if and only if there exists w for which
x = g◦w.
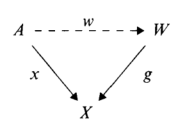
Since most maps g are not split epimorphisms, the problem of which figures are in g is more difficult unless some restriction is made. The most important restriction is to consider only those g which are parts of X; then we use these as tools for investigating the general g via the notion of image.
Definition: An image of a map g is a part i of the codomain of g for which
- g is in i
- for all parts j, if g is in j then i is in j.
Any two images of the same g are uniquely isomorphic as parts.
Inverse images and Truth
Definition: A part j such that for any x, x is in j if only if f◦x is in i is called an inverse
image of i along f.
Definition: An object Omega together with a given part T ->(v)-> Omega is called a subobject
classifier or truth value object for C if and only if for every part g of any X there is exactly one
X ->(r)-> Omega for which g is the inverse image of v along f. The map v with this
remarkable property is often called simply ‘true’. In general, f◦x is called the truth
value of ‘x belongs to g’.
