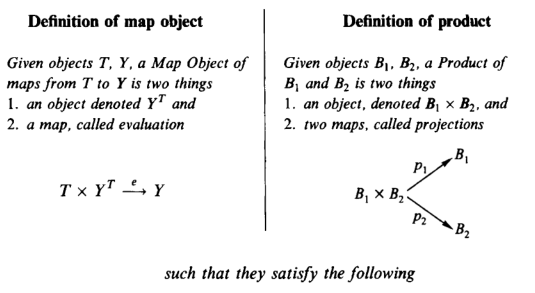
Map objects, or function spaces
Map objects, or function spaces, are also called exponential objects because they satisfy laws of exponents in arithmetric are special cases. They are used to study the way in which an output depends on a whole process, rather than just a single input.
A product of two objects X1 and X2 of a category C can be described as a terminal object in a certain category we constructed from C, X1 and X2. In the same way, given two objects T and Y in C, we can construct a category in which the corresponding map object Y[T] may be described as a terminal object.
Given two objects T and Y of a category C that has a terminal object and products, we define a category C/(T -> Y) by saying that
- an object in C/(T -> Y) is an object X of C together with a map in C from T x X to Y,
- a map in C/(T -> Y) from T x X’ ->(f’)-> Y to T x X ->(f)-> Y is a C-map X’ ->(epsilon)-> X such that f’ = f◦(1T x epsilon).
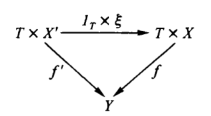
Meaning of 1T x epsilon. If we have any two maps A ->(g)-> B, C ->(h)-> D in a category with products, we can define a map g x h from A x C to B x D by first calculating the two composites A x C ->(proj1)-> A ->(g)-> B, A x C ->(proj2)-> C ->(h)-> D and then forming the pair <g◦proj1, h◦proj2>: A x C -> B x D which we take as the definition of g x h. Thus the map 1T x epsilon is defined by the diagram
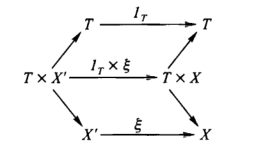
where the unlabeled maps are product projections.
In this category, the identity law is for any object T x X ->(f)-> Y, the identity map is a map from T x X ->(f)-> Y to itself; i.e. f◦(1T x 1X) = f which derives from the fact that the product of identities is another identity, 1T x 1X = 1(T x X). And the map composition is that for any three objects T x X ->(f)-> Y, T x X’ ->(f’)-> Y, and T x X’’ ->(f’’)-> Y, and any two maps in C/(T -> Y), say epsilon form T x X’ ->(f’)-> Y to T x X ->(f)-> Y and eta from T x X’’ ->(f’’)-> Y to T x X’ ->(f’)-> Y, the composite epsilon◦eta (a map of C) is indeed a map in C/(T -> Y) from T x X’’ ->(f’’)-> Y to T x X ->(f)-> Y, i.e. f◦(1T x (epsilon◦eta)) = f’’, which is derived from a sort of ‘distributivity of product with respect to composition’, which takes the form 1T x (epsilon◦eta) = (1T x epsilon)◦(1T x eta).
An object T x X -> Y is a scheme for naming maps from T to Y in C. An example is a processor, where X is the set of names of all the functions that the processor can perform, and T and Y are the sets of all possible inputs and outputs. The map T x X ->(f)-> Y describes the processor itself: f(t, x) is the result of applying the operation whose name is x to the input t. Therefore, for each element x of X, f(-, x) represents a map T -> Y. In particular, taking X to be the terminal object 1 of C, an object T x X -> Y amounts to just a single map T -> Y ‘named’ by 1, because T x 1 is isomorphic to T. Similarly, if X = 2, it names two maps T -> Y, with larger X, the objects X, f can name more maps from T to Y.
A map epsilon from X’, f’ to X, f in C/(T -> Y) is a way to correlate the names of the maps T -> Y as named by X’, f’ with the names of the maps T -> Y as named by X, f. It is a sort of dictionary. The condition for a map X’ ->(epsilon)-> X in C to belong to the category C/(T -> Y) is that for any name x’ in X’, the map f(-, epsilon◦x’) is the same as the map f’(-, x’), i.e. for every element t of T, f(t, epsilon◦x’) = f’(t, x’). This is what is meant by the condition f◦(1T x epsilon) = f’, since by the definition of product of maps (1T x epsilon)(t, x’) = (t, epsilon◦x’).
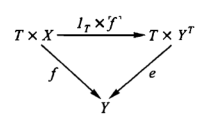
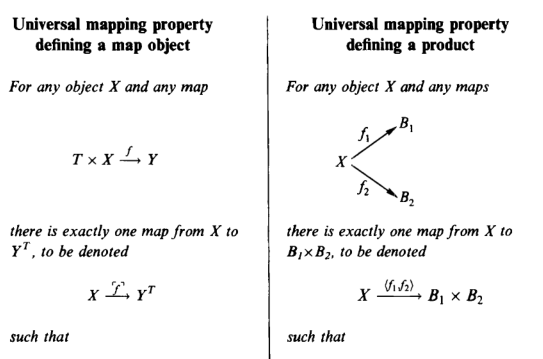
For a given category C, the category C/(T -> Y) associated with some T and Y may have a terminal object. Then the corresponding object of C, denoted by the exponential notation Y[T] (Y raised to the power T) is called the map object from T to Y. The corresponding map of C, T x Y[T] -> Y, is denoted by e or ev and is called the evaluation map. To say that T x Y[T] ->(e)-> Y is a terminal object in C/(T -> Y) means that for every object T x X ->(f)-> Y of this category there is exactly one map of C/(T -> Y) from that object to T x Y[T] ->(e)-> Y. By definition of C/(T -> Y), this is a map X -> Y[T] in C such that
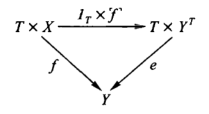
i.e. e◦(1T x ^f^) = f. Thus, to say that T x Y[T] ->(e)-> Y is a terminal object in C/(T -> Y) means, expressed in C: For every map T x X ->(f)-> Y in C there is exactly one map ^f^: X -> Y[T] such that e◦(1T x ^f^) = f.
Having map objects in a category is a strong condition. In many categories C, Y[T] exists only for certain ‘small’ objects T. Best of all are the cartesian closed categories: those categories with products in which every pair of objects has a map object. (‘closed’ refers to the fact that the maps from one object to another do not just form something outside of the category - a set - but form an object of C itself).
P336 there is an excellent example of the transformation of map objects.
Laws of exponents
If the base is a product, the relevant law is (Y1 x Y2)[T] = Y1[T] x Y2[T] and its empty case (product of no factors) 1[T] is isomorphic to 1.
If the exponent is a product, we need (Y[T])[S] is isomorphic to Y[T x S] and its empty case Y is isomorphic to Y[1].
If the exponent is a sum Y[(T1 + T2)] is isomorphic to Y[T1] x Y[T2] and its empty case Y[0] is isomorphic to 1.
The distributive law in cartesian closed categories
Any cartesian closed category satisfies the distributive law, giving the construction of a map T x (X1 + X2) -> T x X1 + T x X2, which can be proved to be inverse to the standard map T x X1 + T x X2 -> T x (X1 + X2). The maps T x (X1 + X2) -> T x X1 + T x X2 ‘are the same’ as the endomaps of T x X1 + T x X2, and it therefore implies that there is a special map T x (X1 + X2) -> T x X1 + T x X2 namely the one that corresponds to the identity of T x X1 + T x X2. This is the map inverse to the standard map T x X1 + T x X2 -> T x (X1 + X2).
Map object versus product
If T and Y are objects in a category with products, the map object of maps from T to Y is two things: a new object, to be denoted Y[T], and a map T x Y[T] -> Y, to be denoted e (for evaluation), satisfying the following universal mapping property. For every object X and every map T x X ->(f)-> Y, there is exactly one map from X to Y[T], to be denoted X ->^f^-> Y[T] which together with e determines f as the composite

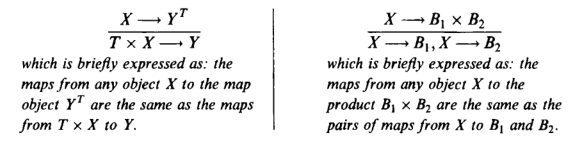
These universal mapping properties can be symbolically summarized as