Notes On Word2vec

In the previous post, I introduce the basic elements of the neural network. The word2vec is a success of the neural network for learning the distributed representations of the words.

The word2vec maps the original word encoded in one-hot vector to another vector. The dimension of the original one-hot vector is very high, usually proportional to the vocabulary of the corpus. Besides, the one-hot vector can barely contain semantic meaning of the word. While the mapped vector has a much lower dimension, usually in hundreds or thousands and contains the semantic meaning of the word, such as \(v_\text{queen} - v_\text{woman} + v_\text{man} \approx v_\text{king}\).

There are two main word2vec models, the skip gram model and the continuous bag-of-words model.

The skip gram model

The input of the skip gram model is a single word \(w_I\), the output is the words in \(w_I\)’s context \(\{w_{O,1}, w_{O,2}, \cdots, w_{O,C}\}\) defined by a window of size \(C\). All of the words are one-hot encoded.

Below is the diagram of the skip gram model.

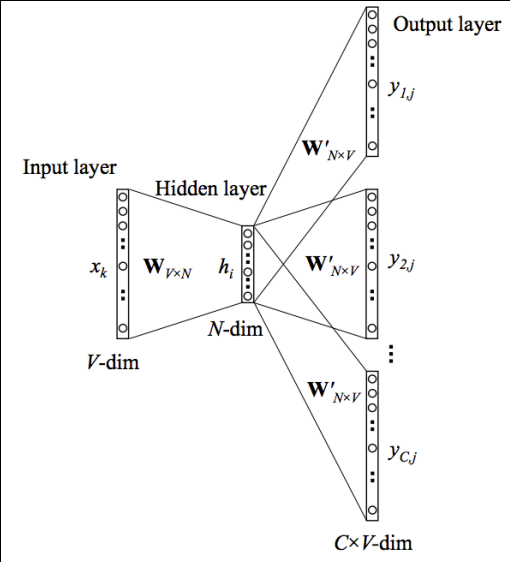
In the diagram, \(\vec x\) and \(\vec y_c\) are one-hot encoded vectors, the \(V\times N\) matrix \(W\) is the weight matrix between the input layer and the hidden layer whose \(i^{th}\) row represents the weights corresponding to the \(i^{th}\) word in the vocabulary. The \(N \times V\) matrix \(W’\) is the parameter between the hidden layer and the output layer. The output layer is a softmax regression.

The vector in the hidden layer is the distributed representation of the input word, suppose \(w_I = \vec x\) is the \(k^{th}\) word in the vocabulary:

$$\vec h = \vec x W = W_{k,*} := v_{w_I}$$

The output of the model is:

$$P(w_{c,j} = w_{O,c} | w_I) = \frac{e^{v_{w_I}v'_{w_j}}}{\sum_{v=1}^V e^{v_{w_I}v'_{w_v}}}$$

The continuous bag-of-words model

The continuous bag-of-words model is like the skip gram model with the input and output reversed.

The input is the one-hot encoded context words \(\{x_1, x_2, \cdots, x_C\}\) for a window of size \(C\), the output is a one-hot encoded word.

Below is the diagram of the continuous bag-of-words model.

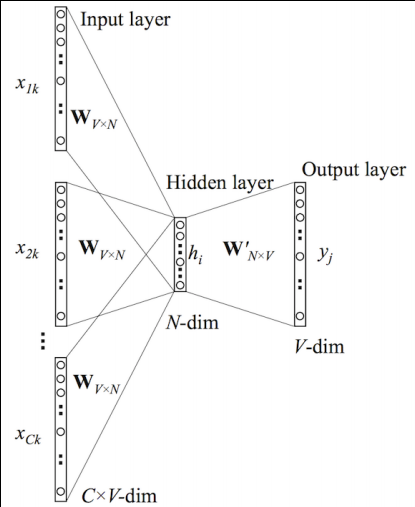
In the diagram, \(\vec x_c\) and \(\vec y\) are one-hot encoded vectors, the \(V\times N\) matrix \(W\) is the weight matrix between the input layer and the hidden layer whose \(i^{th}\) row represents the weights corresponding to the \(i^{th}\) word in the vocabulary. The \(N \times V\) matrix \(W’\) is the parameter between the hidden layer and the output layer. The output layer is a softmax regression.

The vector in the hidden layer is average of the distributed representation of the input words:

$$\vec h = \frac{1}{C} \sum_{c=1}^C \vec x_c W = \frac{1}{C} \sum_{c=1}^C \vec x_c v_{x_c}$$

The output of the model is:

$$y_i = P(w_{y_i} | w_1, w_2, \cdots, w_C) = \frac{e^{\vec h \vec v'_{w_i}}}{\sum_{j=1}^C \vec h \vec v'_{w_j}}$$

The parameter of both the skip gram model and the continuous bag-of-words model can be learnt with the backpropagation algorithm.

The previous posts softmax regression revisit and softmax regression revisit 2 describe the methods to reduce the computational complexity during the model training.

After learning the model, we calculate the distributed representation of word by selecting the corresponding row in the matrix \(W\).