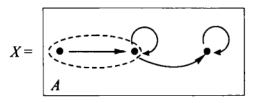
Parts and inclusions
If X is a given object of a category C, we can form anoter category C/X: an object of C/X is a map of e with codomain X, and a map from an object A = (A0 ->alpha X) to an object B = (B0 ->beta-> X) is a map of C from A0 to B0 which beta takes to alpha, i.e. a map A0 ->(f)-> B0 such that beta◦f = alpha:
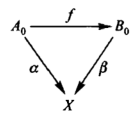
We obtain a catgory, because if we have another map
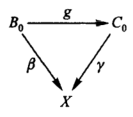
i.e. gamma◦g = beta, then g◦f is also a map in C/X since gamma◦gf = alpha.
We want to define a part of this category, denoted by P(X), P(X) less than (c=) C/X, which is called the category of parts of X. The objects of P(X)f are all objects alpha of C/X which are inclusion maps in C, i.e. the objects of P(X) are the parts or subobjects of X in C. The maps of P(X) are all maps between its objects in C/X; given any two objects A0 ->(alpha)-> X and B0 ->(beta)-> X in P(X), there is at most one map A0 ->(f)-> beta0 in C such that beta◦f = alpha.
If the category C has a terminal object 1, then we can form the category C/1, but this turns out to be none other than C, since it has one object for each object of C and its maps are precisely the maps of C. Therefore the category of parts of 1, P(1), is a subcategory of C, precisely the subcategory determined by those objects A0 whose unique map A0 -> 1 is injective. Thus while a subobject of a general object X involves both an object A0 and a map A0 ->(alpha)-> X, when X = 1 only A0 need be specified, so that ‘to be a part of 1’ can be regarded as a property of the object A0, rather than as an additional structure alpha.
Given any two objects A c->(alpha)-> X, and B c->(beta)-> X in P(X) there is at most one map A ->(f)-> B in C such that beta◦f = alpha. For any two of its object there is at most one map from the first to the second. A category which has this property is called a preorder. Thus, the category of subobjects of a given object in any category is a preorder.
To know the category of subobjects of a given object X, we need only know, for each pair of subobjects of X, whether there is or there is not a map from the first to the second. To indicate that there is a map (necessarily unique) from a subobject A c->(alpha)-> X to a subobject B c->(beta)-> X we often use the notation A less than (X) B; the A is an abbreviation for the pair A, alpha, and similarly for B. The X helps remind us of that.
If A less than (X) B and B less than (X) A then A is isomorphic to (X) B.
Toposes and logic
Definition: A category C is a topos if and only if:
- C has 0, 1, x, +, and for every object X, C/X has products.
- C has map objects Y[X]
- C has a truth-value object 1 -> Omega
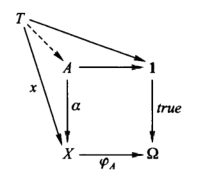
The defining property of a truth-value object or subobject classifier 1 ->(true)-> Omega was that for any object X the maps X -> Omega are ‘the same’ as the subobjects of X. This means that for each subobject, A c->(alpha)-> X of X there is exactly one map X ->(phiA)-> Omega having the property that for each figure T ->(x)-> X, phiA◦x = trueT if and only if the figure x is included in the part A c->(alpha)-> X of X.
Forming the product Omega x Omega and defining the map 1 ->(<true, true>)-> Omega x Omega. This is injective because any map whose domain is terminal is injective; therefore this is actually a subobject and it has a classifying or characteristic map Omega x Omega -> Omega. This classifying map is the logical operation ‘and’, denoted as ‘&’ and ‘^’. The property of this operation is that for any T ->(a)-> Omega x Omega, say a = <b, c> where b and c are maps from T to Omega, the composite has the property that b ^ c = trueT if and only if <b, c> belongs to <true, true>, which means precisely: b = trueT and c = trueT.
Because b is a map whose codomain is Omega, by the defining property of Omega it must be the classifying map of some subobject of T, B c-> T. In the same way, c is the classifying map of some other subobject, C c-> T, and the subobject classified by b ^ c is called the intersection of B and C.
Another logical operatioin is ‘impilcation’ which is denoted ‘=>’. This is also a map Omega x Omega -> Omega, defined as the classifying map of the subobject S c-> Omega x Omega determined by all those <alpha, beta> in Omega x Omega such that alpha belongs to beta.
There is a third logical operation called ‘or’ and denoted ‘v’, and there are relations among the operations ^, =>, v, which are completely analogous to the relations among the categorical operations x, map object, and +.

It is also possible to define an operation of negation by not phi = [phi => false].
Then phi ^ not phi = false, and the inclusion phi belongs to not not phi. The universal property for => implies that for any subobject A of an object X, not A is the subobject of X which is largest among all subobjects whose intersection with A is empty.